画像をダウンロード 1次関���の利用 280115-1次関数の利��� 応用問題
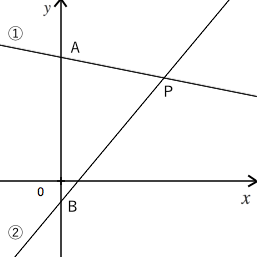
一次関数 グラフを使った問題 苦手な数学を簡単に
日常で使える数学 (1次関数編) なんか変なシリーズができそうです。 僕、中高大とガチガチの文系です。 なんでそんな僕がこんな記事を書こうかとおもったのか。 それは、 「どうせこんなの勉 まとめ:一次関数のグラフと関連用語をマスターしよう! いかがでしたか? 一次関数のグラフの問題1つで色々な問題のパターンを作ることができ、難易度も様々です。 でも、どんな
1次関数の利用 応用問題
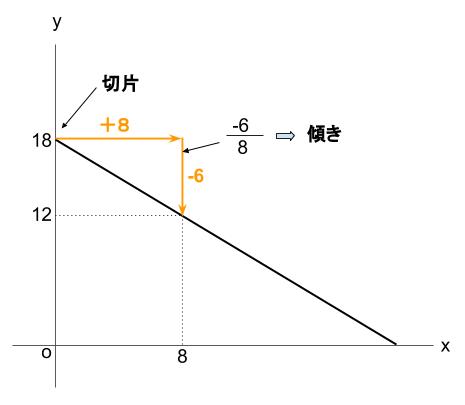
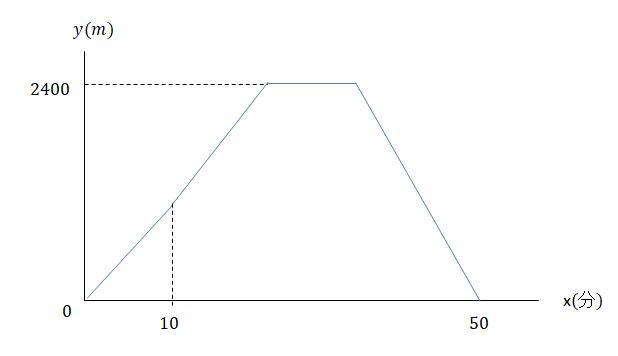
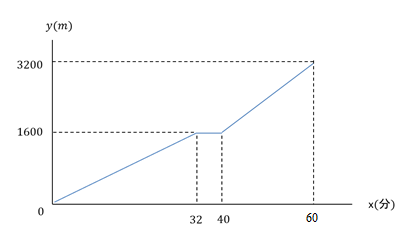
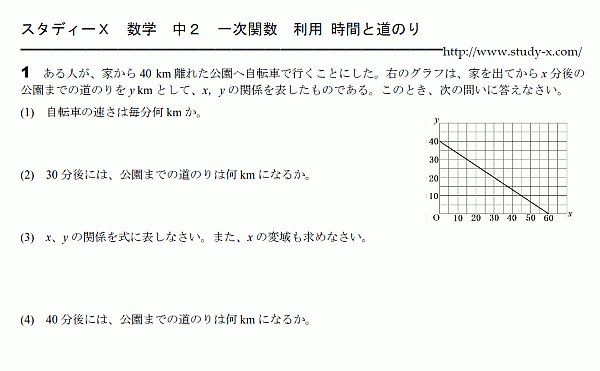
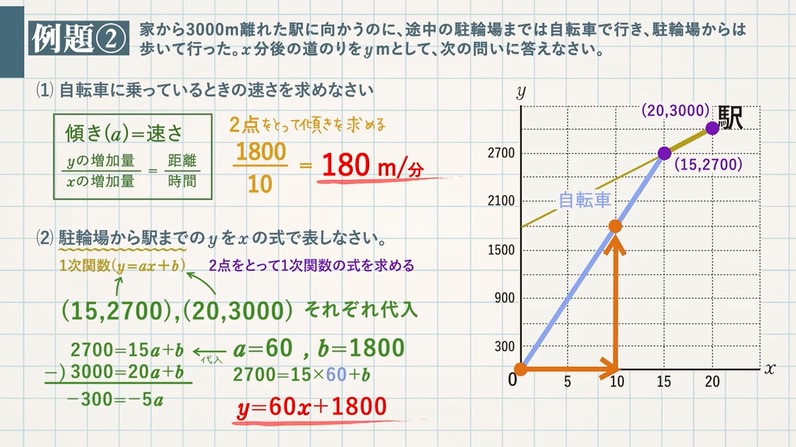
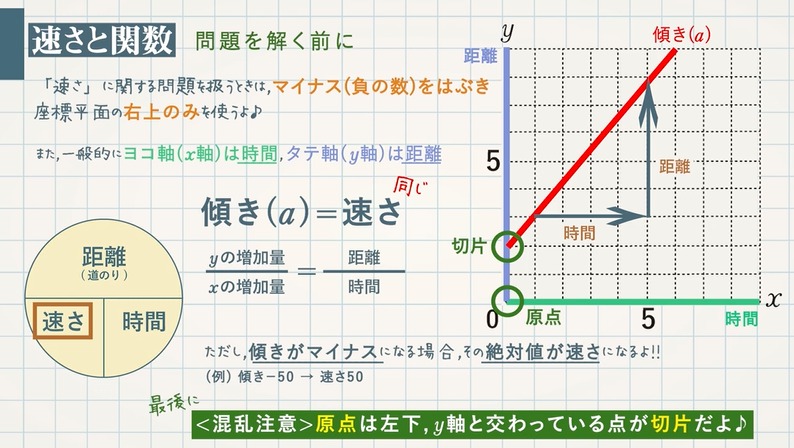
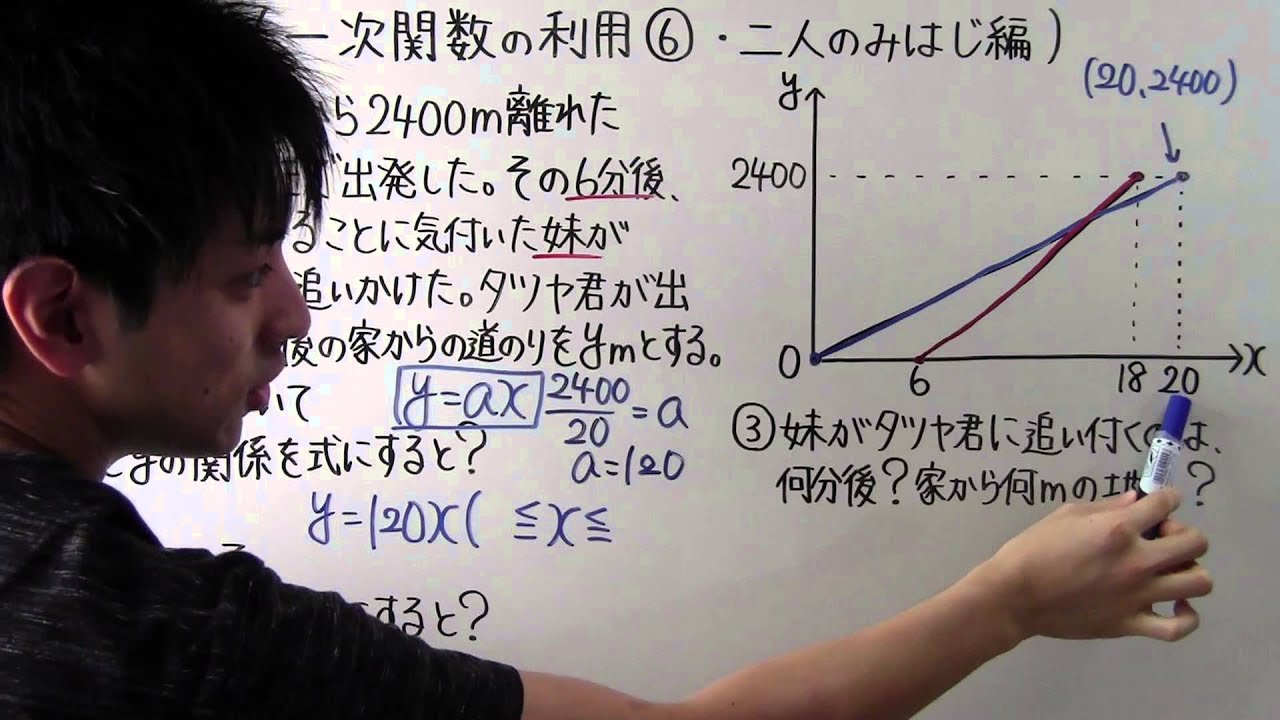
1次関数の利用 応用問題- 数学の関数について。 1次関数の変化の割合 (傾き)を求めるとき、連立方程式を使うと時間がかかるため、 yの増加量/xの増加量で求めたいのですが、引く順番などが分かりません。 説第3章 一次関数 <前: L25 一次関数の利用(2)の問題 L26 一次関数の利用(3)の解答 :次> 練習問題1 アイさんは家から図書館までの道のり4500mを、自転車で毎分300mの速さで進み

数学 中2 41 一次関数の利用 ばねとろうそく編 Youtube
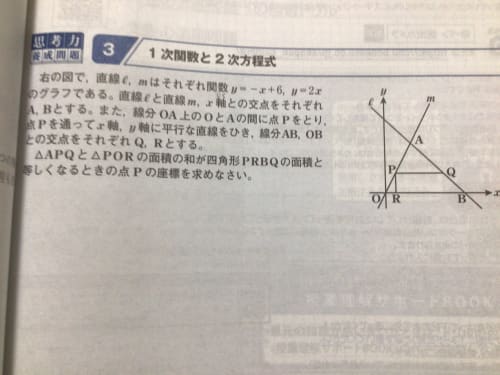
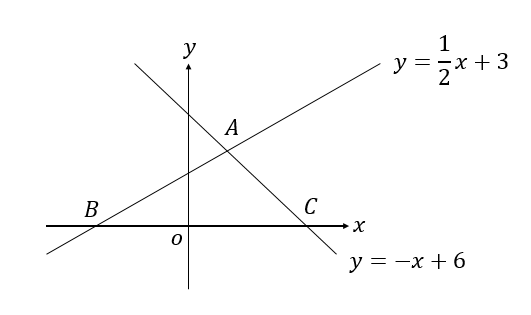
LINE 今回は中2で学習する 『一次関数』の単元から 直線の式の求め方について解説していくよ! ここでは、いろんなパターンの問題が出題されるので パターン別に例題を使って解説していきます。1次関数とは yをxの1次式で表せる関数のことである。 1次関数の式 y=axb a,bは定数 確認 次の中から1次関数をすべて選べ。 答表示 y = 5x 2 y = 3x 2 y= x 2 y = 3 x 12x2y4=0 1次関数の式を1次関数のグラフの応用問題や難問|中学数学~高校入試 – 坂田先生のブログ 100名以上指導したオンライン家庭教師 計算問題の難問 因数分解難問 円 三平方 文章題テーマ別 平方根応用 2次方程式難
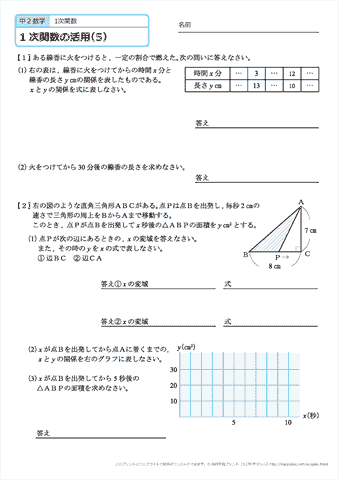
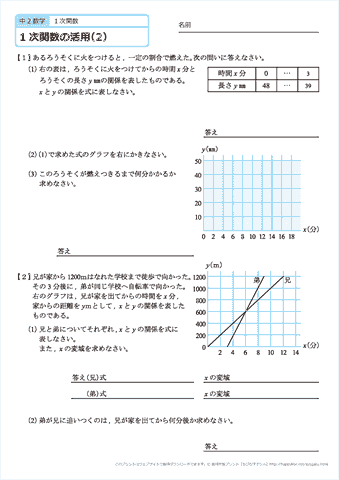
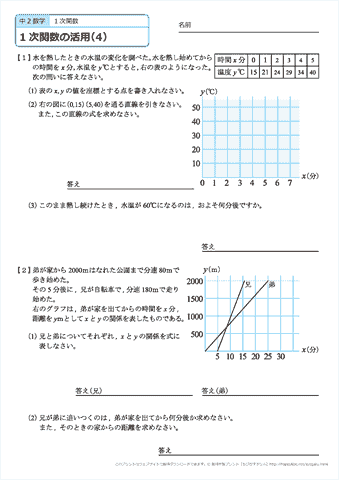
「一次関数の利用の問題について、解き方のコツ」を紹介します。 コツ→3つのパターン 一次関数の利用の問題で最も重要なのは、どの値を「x」「y」とおくかです。 これを間違えなければ、プリントは追加、変更していきます。また、問題の解説も今後増やしていきます。式の計算 単項式と多項式 式の加法・減法 単項式の乗法・除法 いろいろな計算 等式の変形 式の値式の計算の利用 式1次関数がわからない人へ 中2数学「1次関数」がわからない人は、以下の順でTry ITの映像授業を観て勉強してみてください。 「1次関数の式とグラフ」に関する9のポイントを覚える 「1次関数の利
1次関数の利用 応用問題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  |  |
 |  |  |
 |  | |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 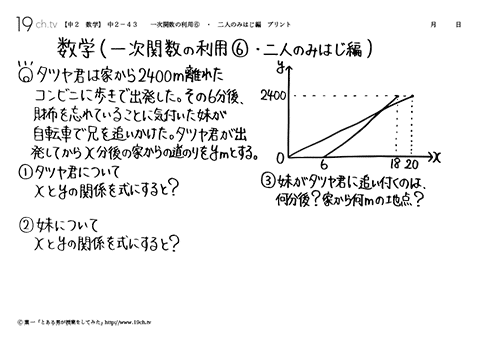 |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 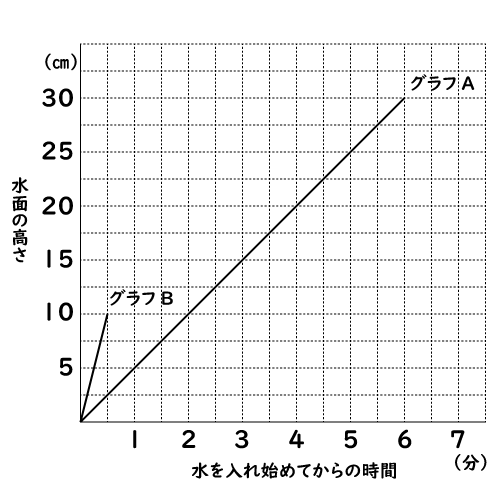 | |
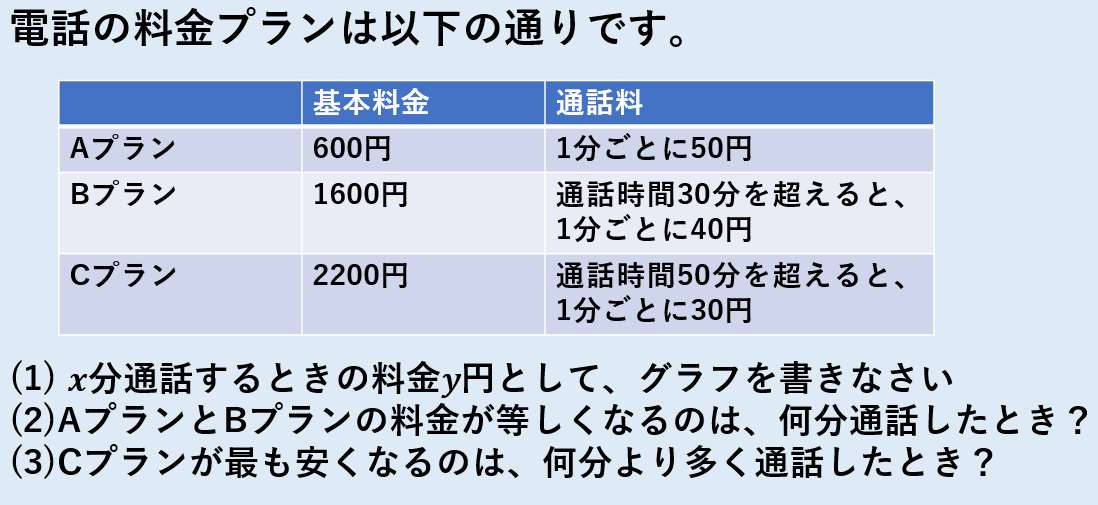 |  | |
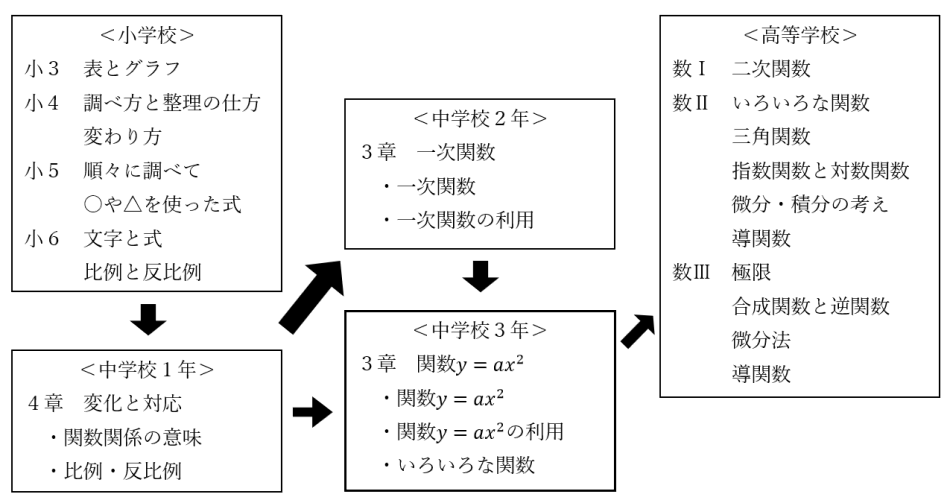 | 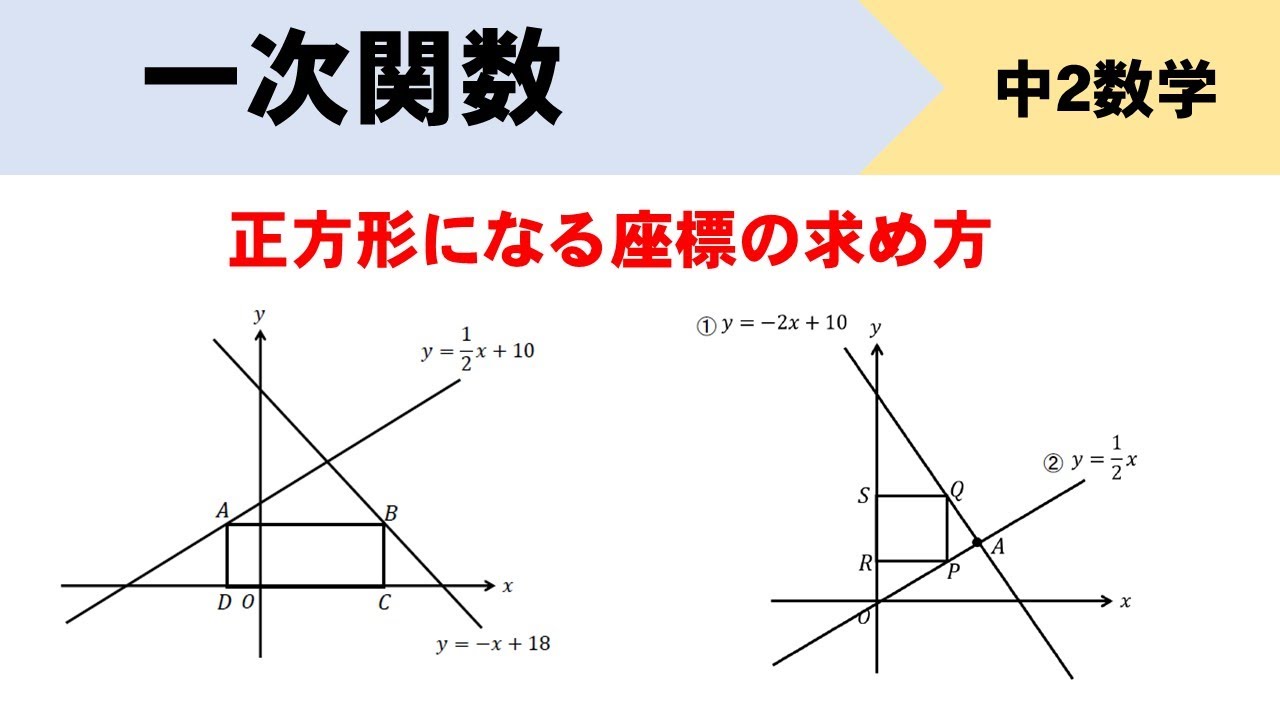 |  |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 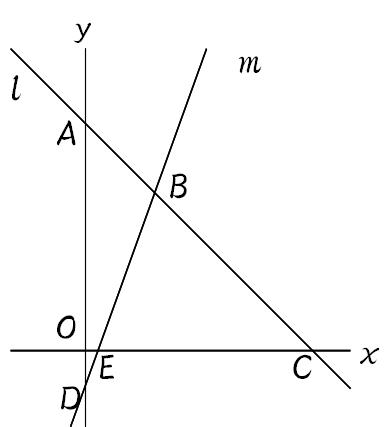 | |
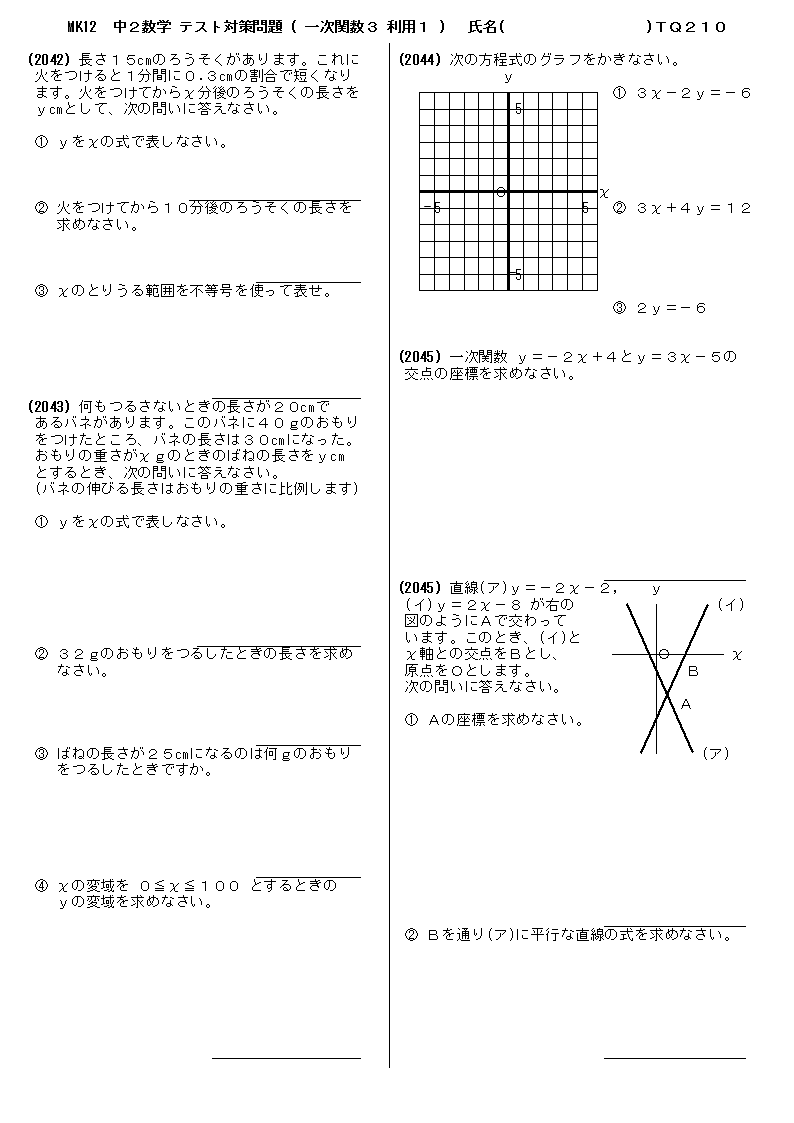 | 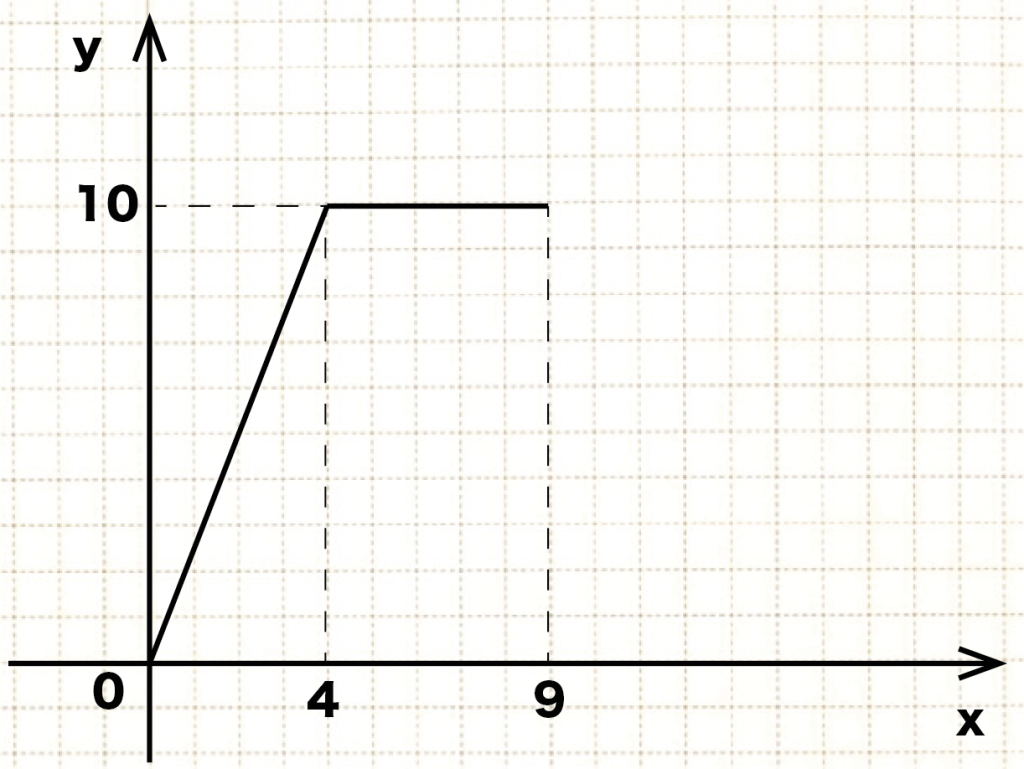 |  |
 |  |  |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | 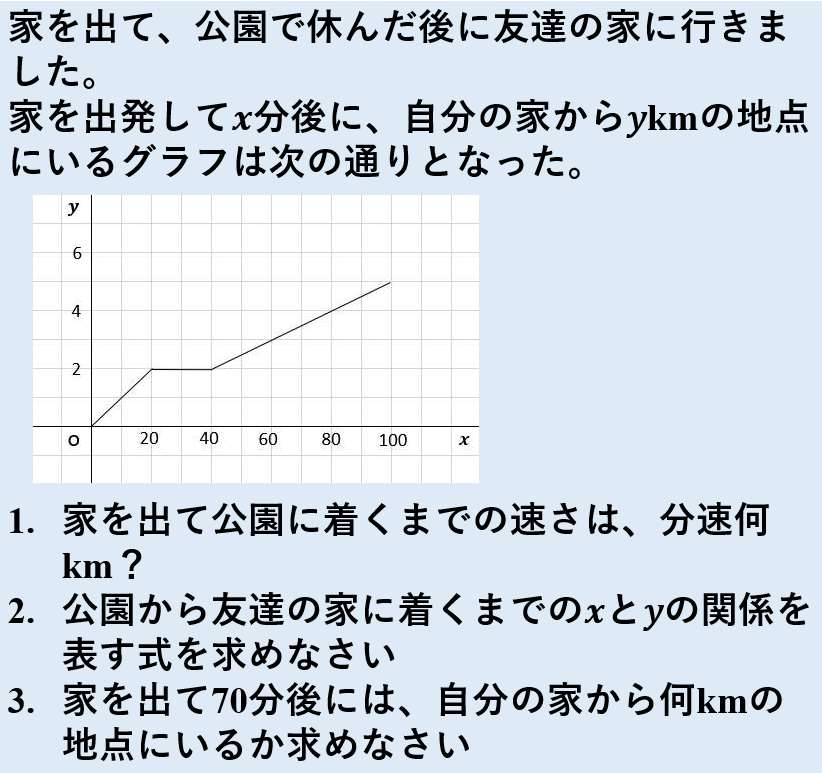 |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
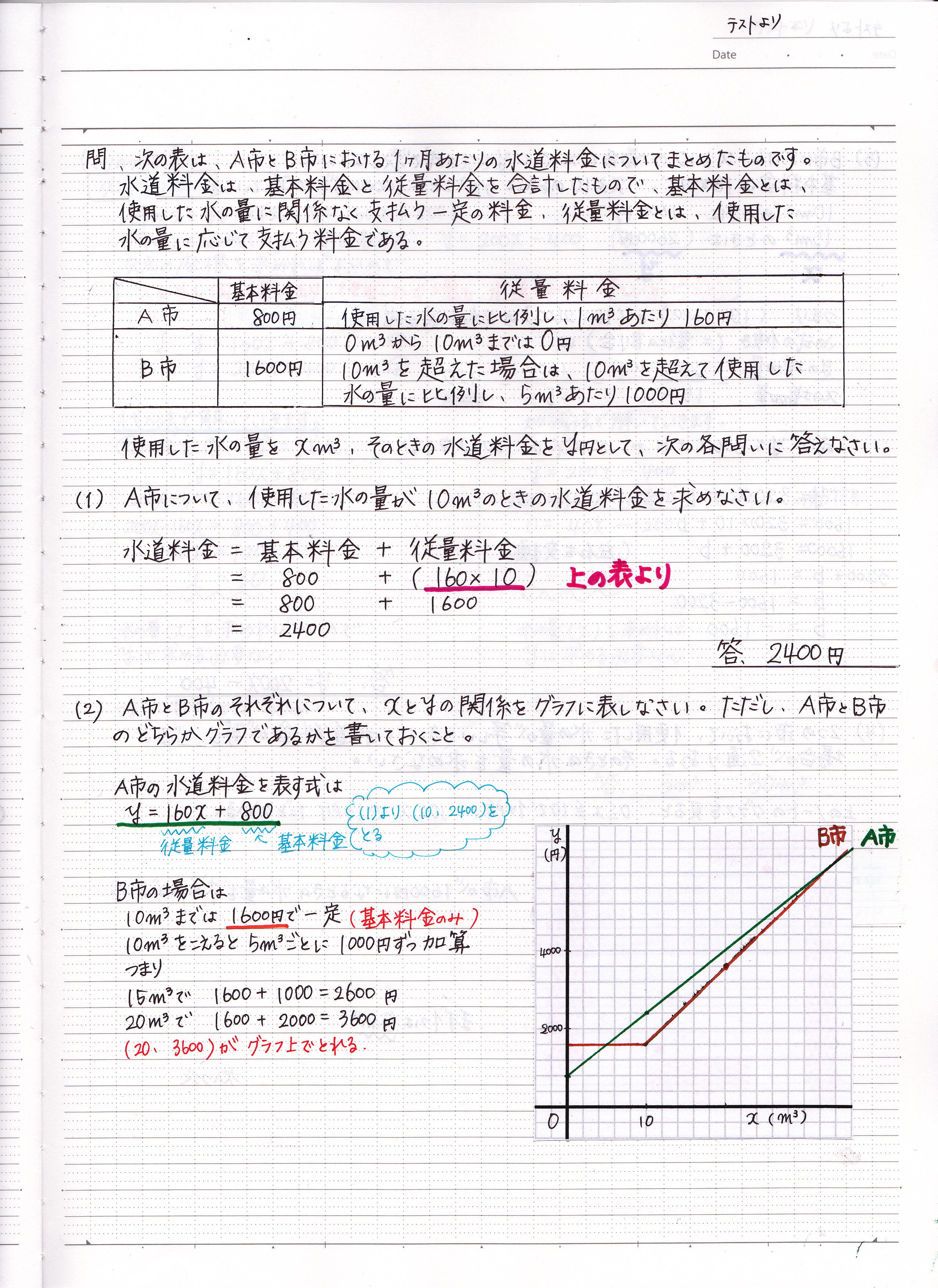 | 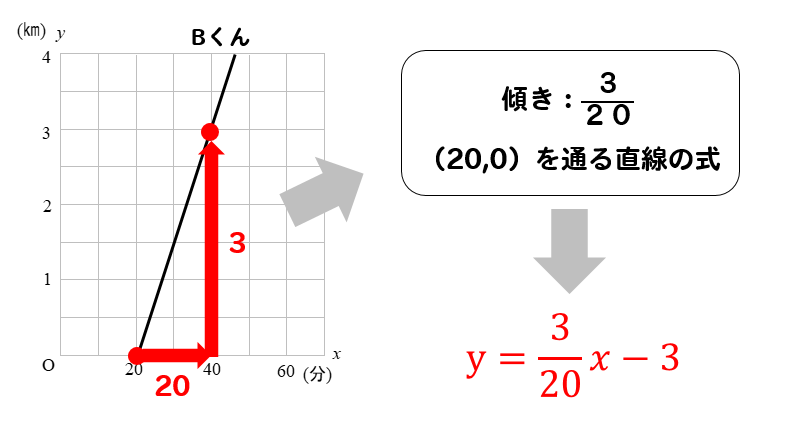 |  |
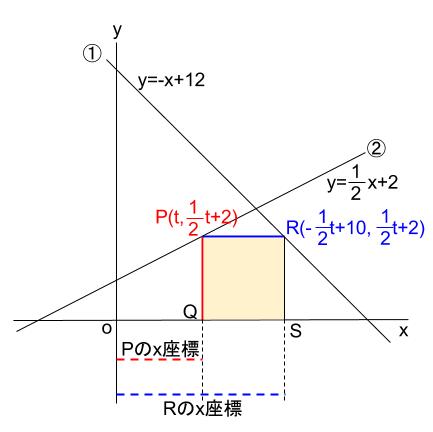 |  |  |
 |  |  |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
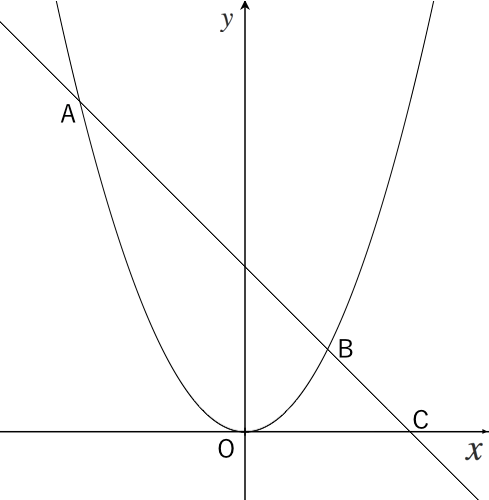 | 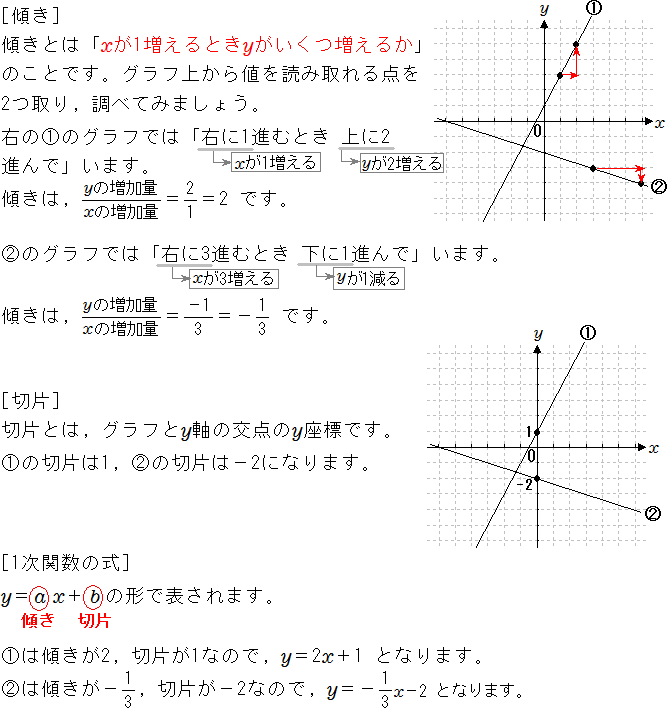 | |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
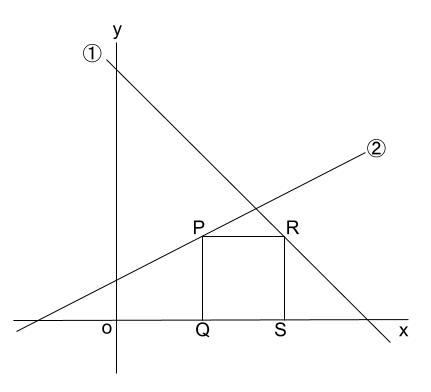 | 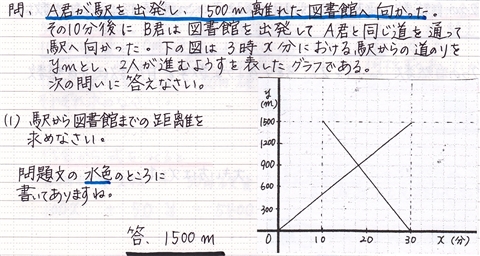 |  |
 |  |  |
 |  |  |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「1次関数の利用 応用問題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | 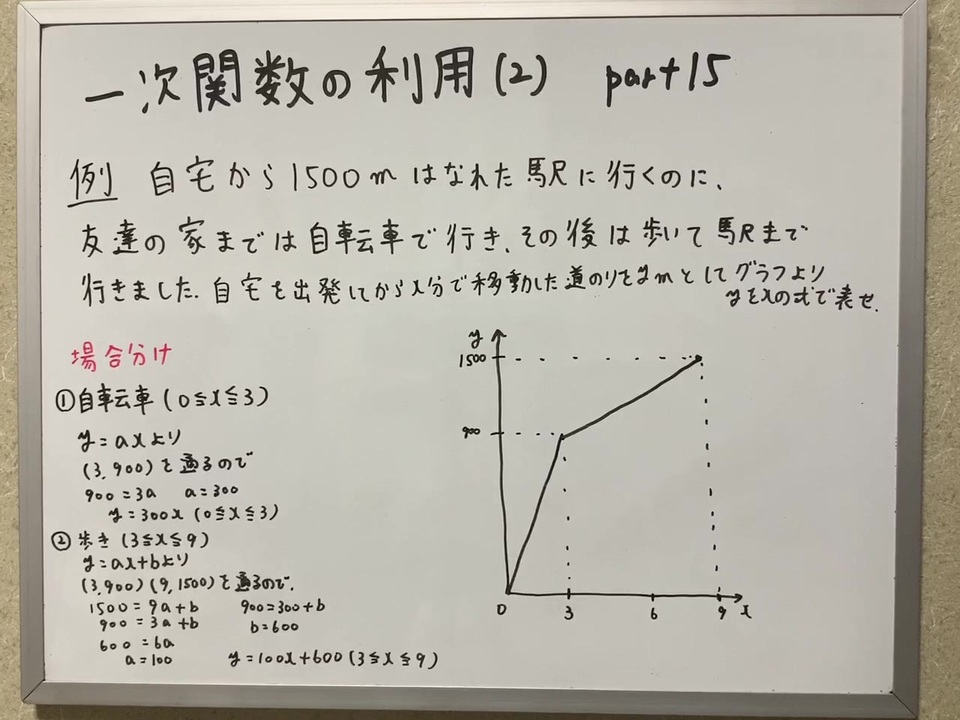 |
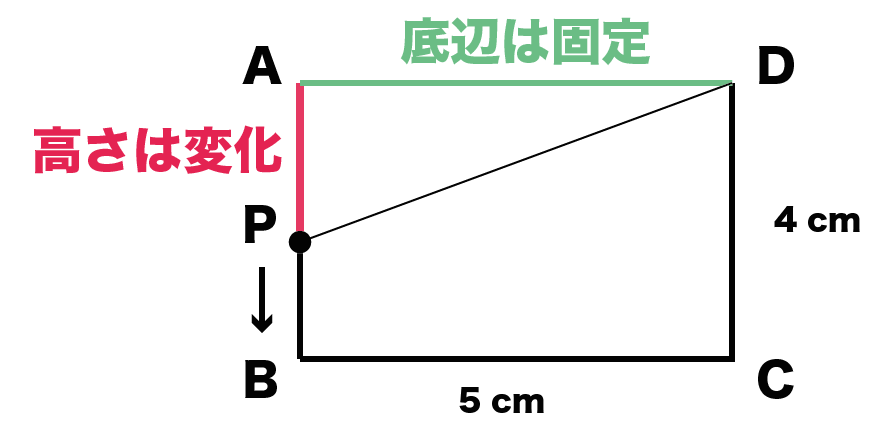 |
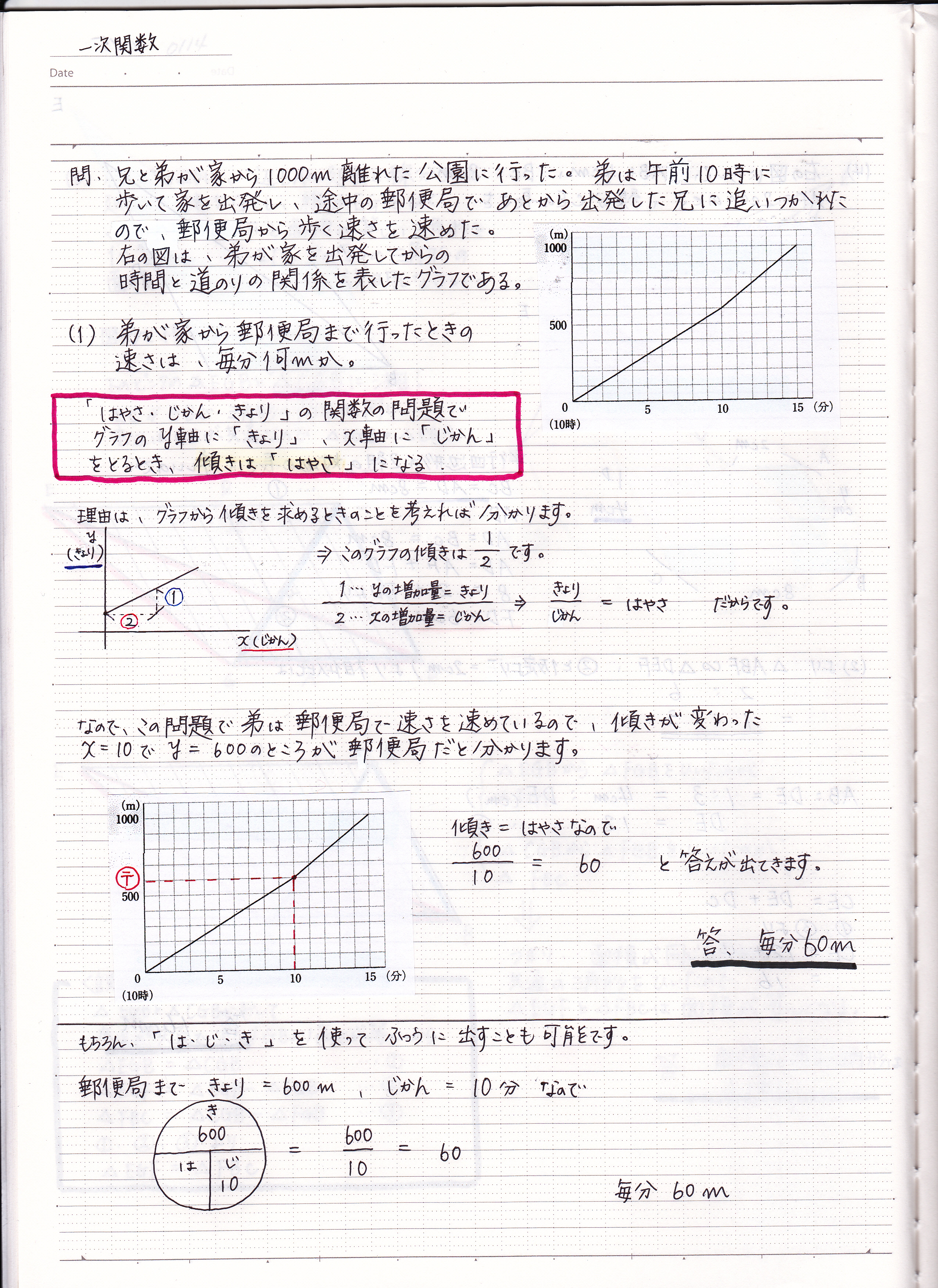
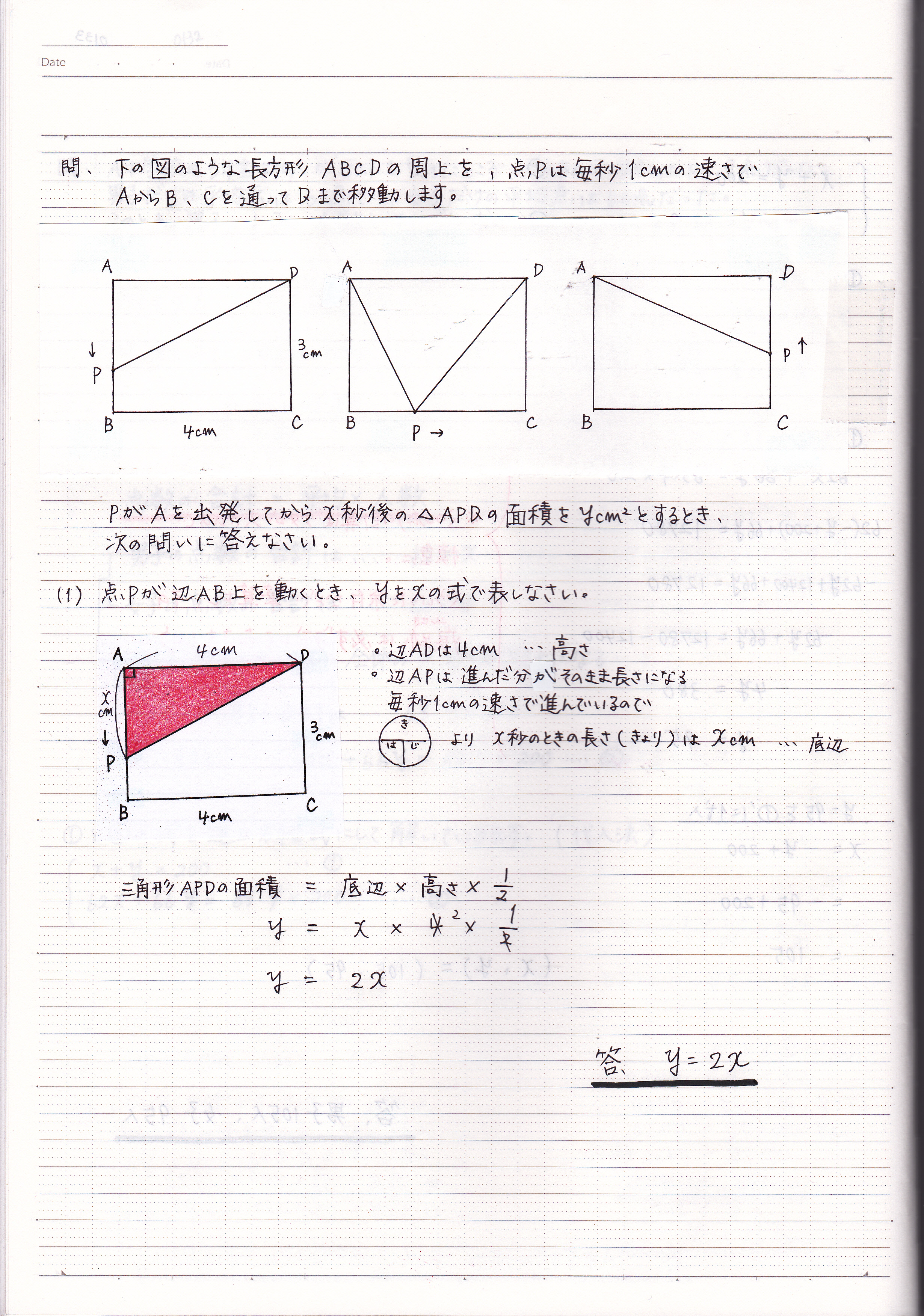
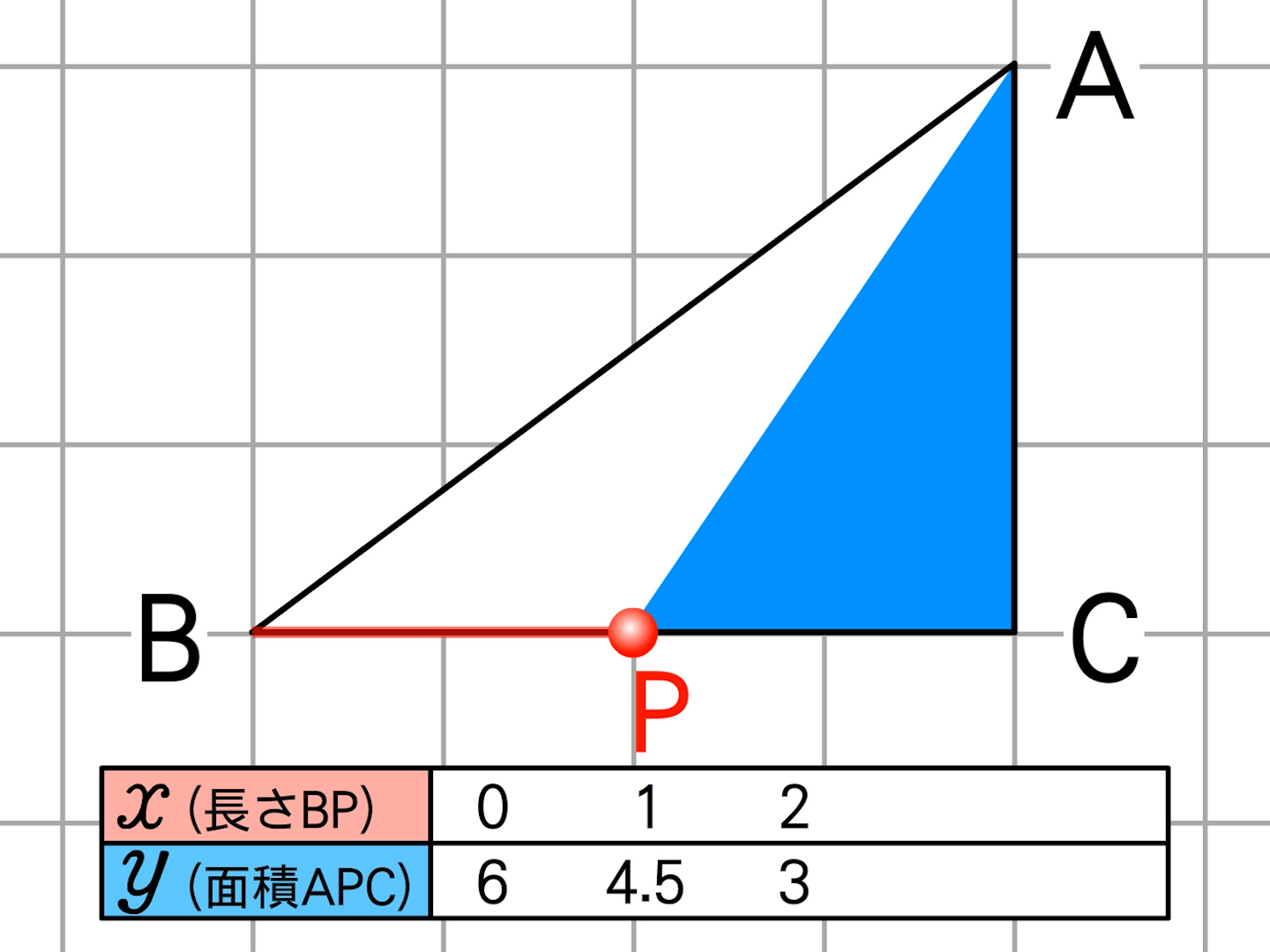
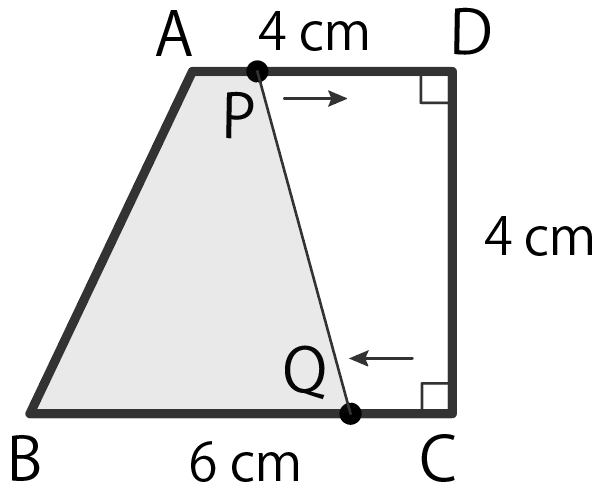
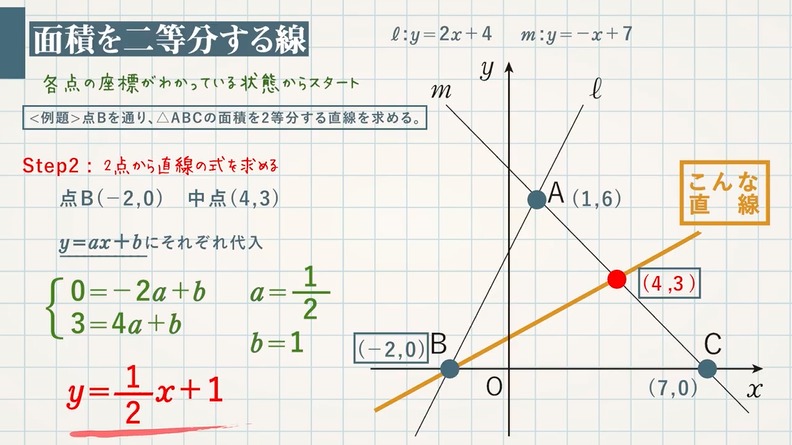
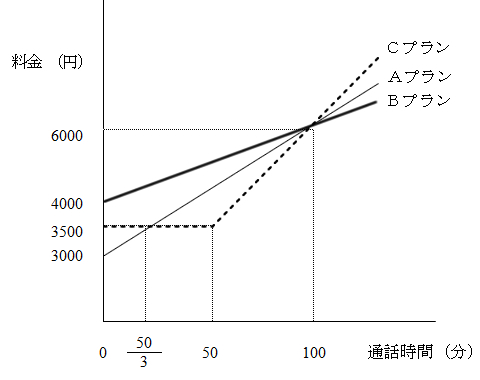
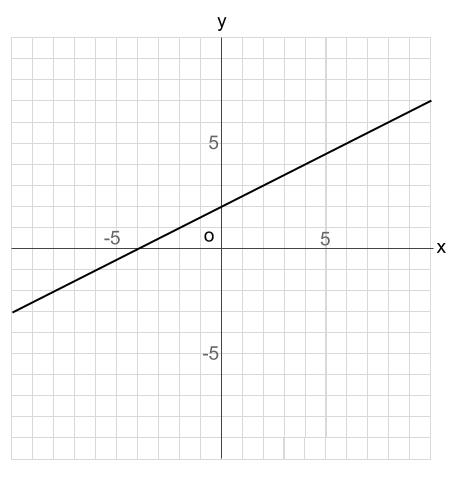
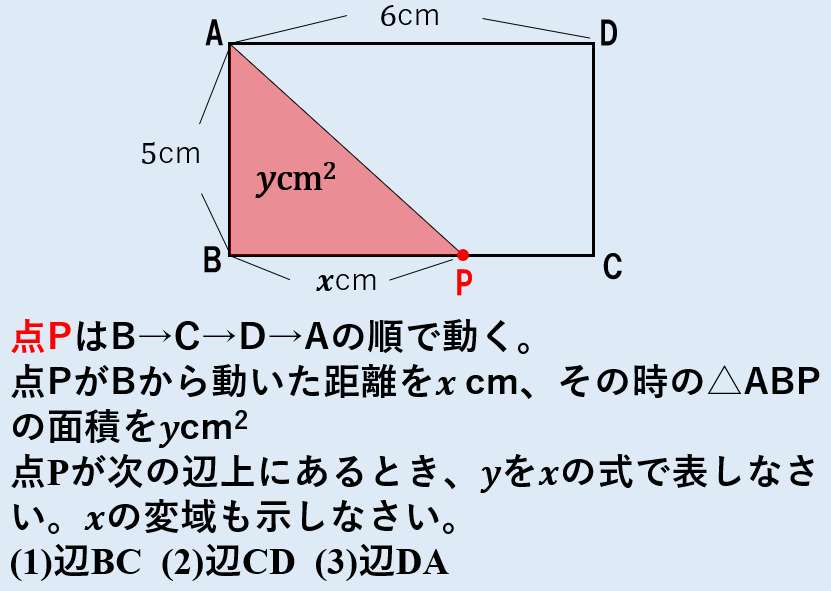
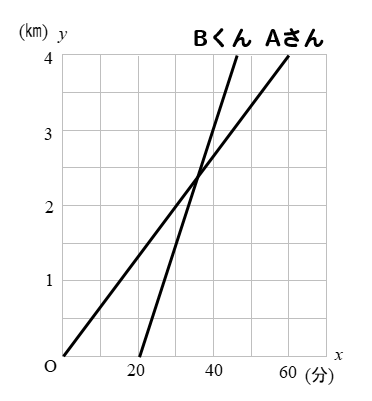
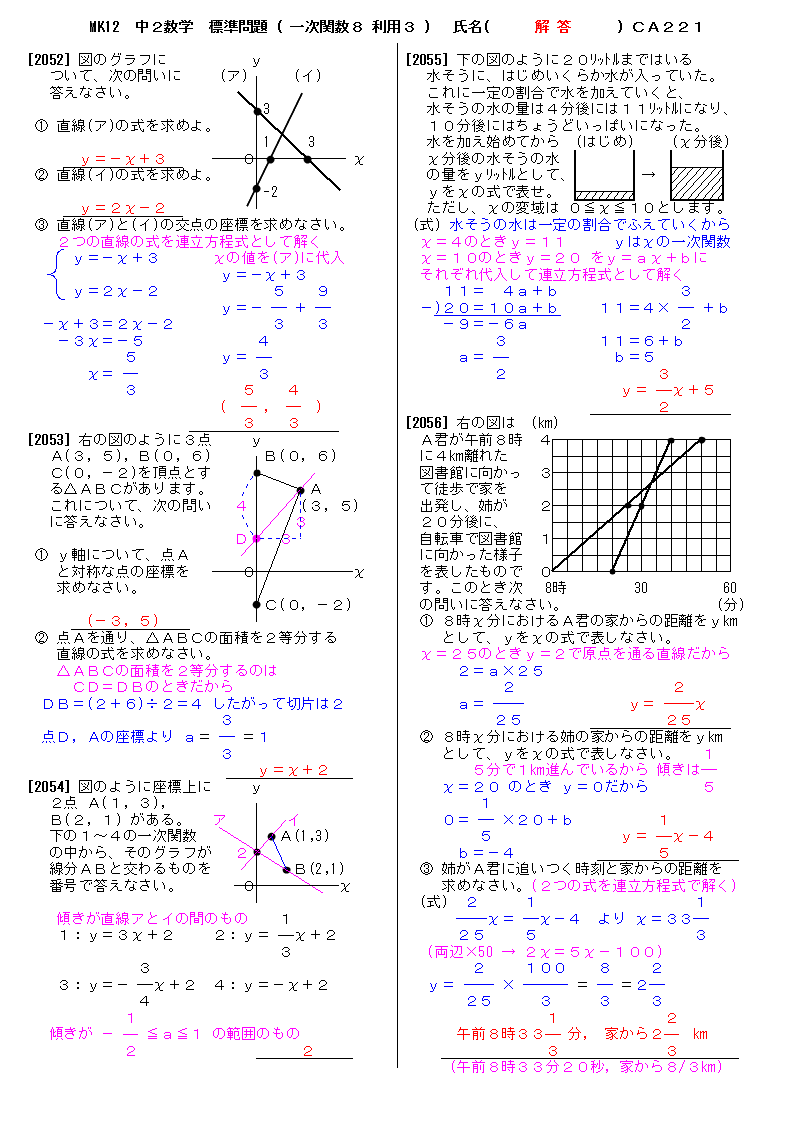
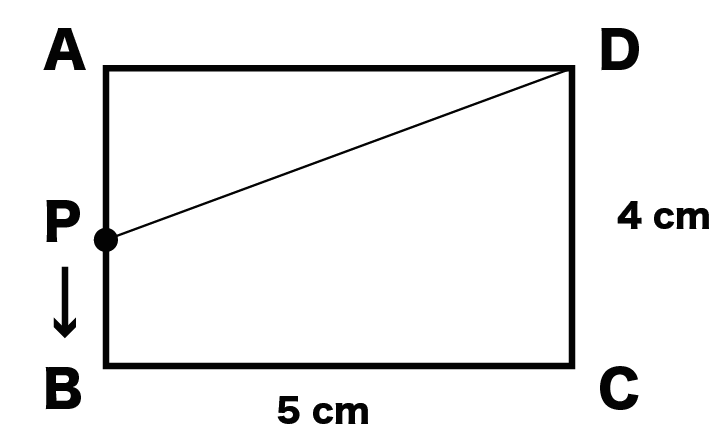
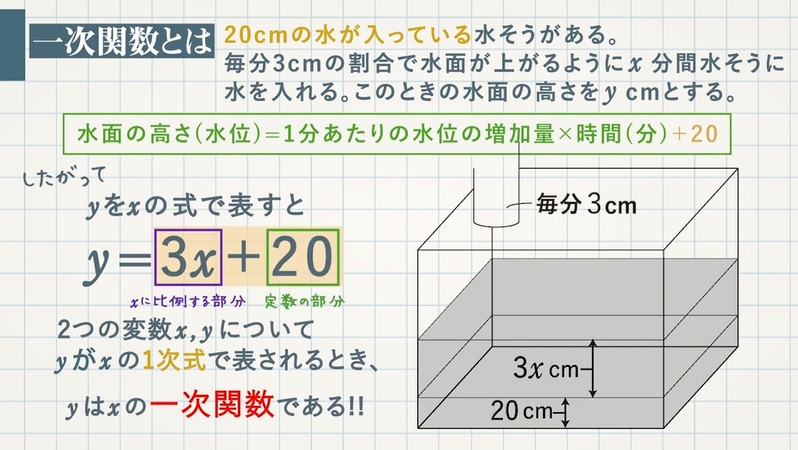
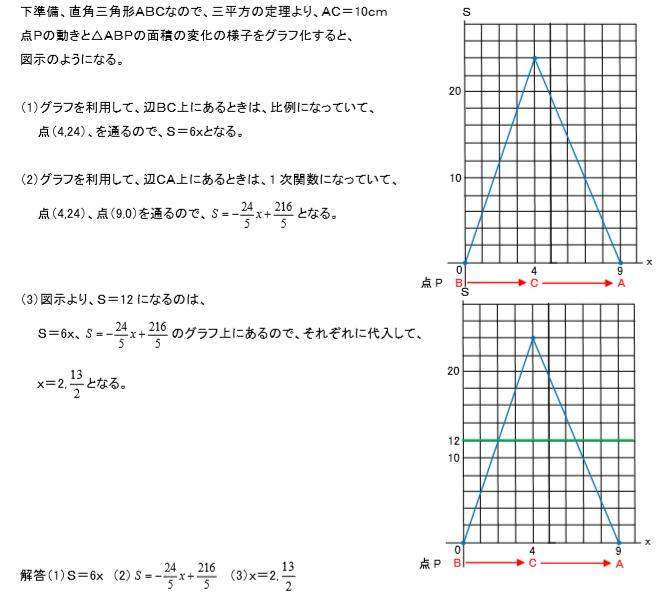
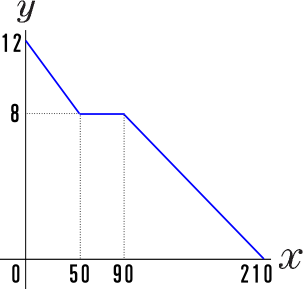
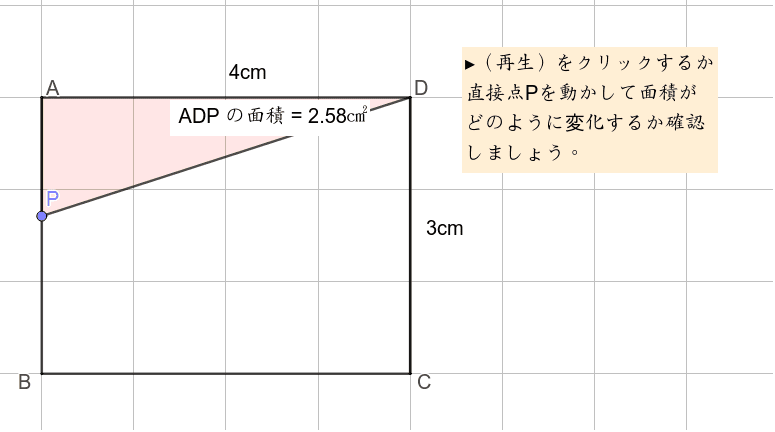
このグラフの1次関数の式は、 \(y=2x2\) になるってことだね。 ②条件から式を求める 1 変化の割合がわかっていて、\(x\)と\(y\)の値がわかっていた場合でも 1次関数の式を求められ1次関数の利用 (動点) 1次関数の応用では 変数x,yがそれぞれ「何を表しているのか」しっかり把握することが大切である。 さらに、動点の問題では 点が動いた道のり をxで表す必要がある。 また、点
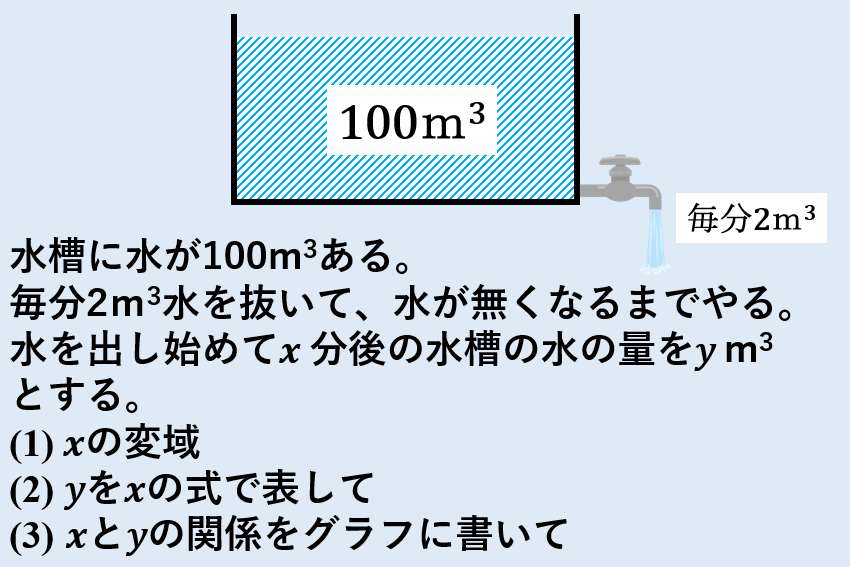
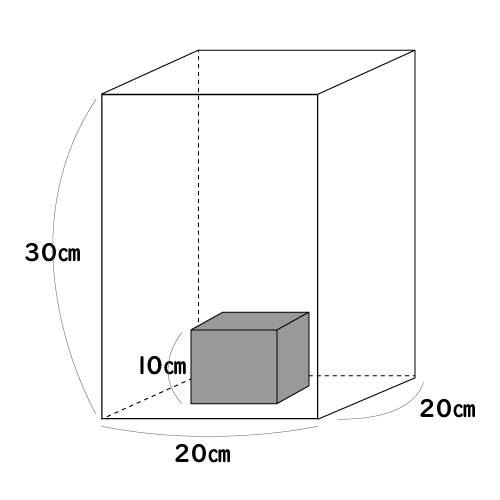
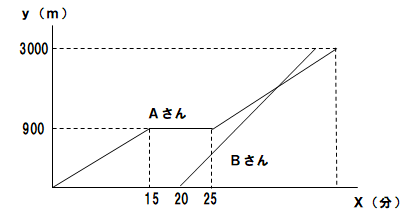
Incoming Term: 1次関数の利用, 1次関数の利用 問題, 1次関数の利用 グラフ, 1次関数の利用 速さ, 1次関数の利用 三角形, 1次関数の利用 動点, 1次関数の利用 水槽, 1次関数の利用 コツ, 1次関数の利用 難問, 1次関数の利用 応用問題,
コメント
コメントを投稿